1 什么是扫描线
在 Oi 中,扫描线通常用于解决二维平面上的矩形面积并问题
前置知识:
- 线段树
- 离散化(有的题目不需要)
1.1 矩形面积并
在一个平面直角坐标系中,有多个矩形,现在询问这些矩形总共覆盖了多少面积
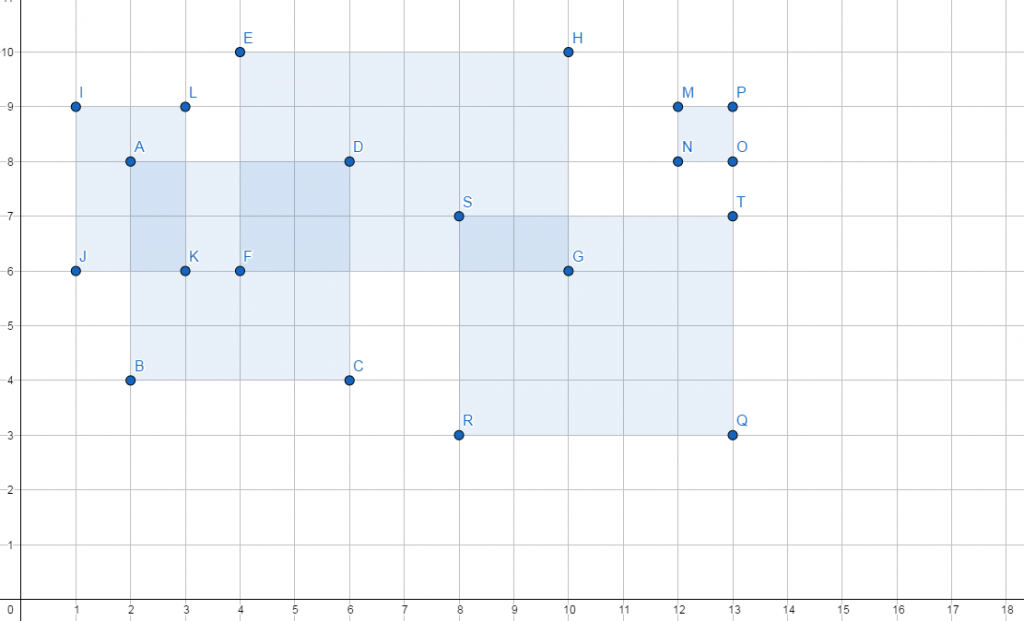
1.2 扫描线
由于矩形之间可能存在互相覆盖的情况
直接朴素的算法复杂度非常的低
我们可以考虑做将图形以 $y$ 坐表分成多行

考虑分别计算每一行的面积
这显然是 $ O(n ^ 2) $
但是每一行可以使用线段树维护
即将线段树视为一条线,从 $y = 0$ 向上扫描
然后将每个矩形拆分成两条线段 —— 下面的边和上面的边
扫描到下面的边所在区间 +1, 否则 -1,累加在每一行时线段树查询所得结果即为答案
这就是扫描线
2 线段树的问题
扫描线有一个非常重要的问题
即我们线段树应当如何维护
2.1 方案 1
每个节点维护两个值 len cnt
len 表示当前区间所有有值的个数
cnt 表示当前区间被加了几次
每次只 PushUp,不进行 PushDown
int tree[N << 2], tree_cnt[N << 2];
inline void push_up( int now, int left, int rig ) {
if( tree_cnt[now] )
tree[now] = ( rig - left + 1 );
else if( rig - left == 0 )
tree[now] = 0;
else
tree[now] = tree[ now << 1 ] + tree[ now << 1 | 1 ];
}
void query_add( int from, int to, int val, int now, int left, int rig ) {
if( from <= left && rig <= to ) {
tree_cnt[now] += val;
push_up( now, left, rig );
return ;
}
int mid = ( left + rig ) >> 1;
if( from <= mid )
query_add( from, to, val, now << 1, left, mid );
if( to > mid )
query_add( from, to, val, now << 1 | 1, mid + 1, rig );
push_up( now, left, rig );
}这份代码中,Tree 表示 len, Tree_cnt 表示 cnt
由于我们只查询 tree[1] ,并且保证先加后减,因此这个做法是对的
2.2 方案 2
这个方法具用更加强的普遍性
通过对 PushUp 和 PushDown 的魔改,使得在这里线段树可以像平常一样使用
int tree[N << 2], lazy[N << 2];
inline void calc( int now, int left, int rig ) {
if( lazy[now] )
tree[now] = ( rig - left + 1 );
else if( rig - left == 0 )
tree[now] = 0;
else
tree[now] = tree[ now << 1 ] + tree[ now << 1 | 1 ];
}
inline void pushup( int now, int left, int rig ) {
if( lazy[now << 1] && lazy[ now << 1 | 1 ] ) {
int tmp = Min( lazy[now << 1], lazy[ now << 1 | 1 ] );
lazy[now] = tmp;
lazy[ now << 1 ] -= tmp;
lazy[ now << 1 | 1 ] -= tmp;
int mid = ( left + rig ) >> 1;
calc( now << 1, left, mid );
calc( now << 1 | 1, mid + 1, rig );
}
}
inline void pushdown( int now, int left, int rig ) {
if( lazy[now] ) {
int mid = ( left + rig ) >> 1;
lazy[ now << 1 ] += lazy[now];
lazy[ now << 1 | 1 ] += lazy[now];
calc( now << 1, left, mid );
calc( now << 1 | 1, mid + 1, rig );
lazy[now] = 0;
calc( now, left, rig );
}
}
void query_add( int from, int to, int val, int now, int left, int rig ) {
if( from <= left && rig <= to ) {
lazy[now] += val;
calc( now, left, rig );
return ;
}
int mid = ( left + rig ) >> 1;
pushdown( now, left, rig );
if( from <= mid )
query_add( from, to, val, now << 1, left, mid );
if( to > mid )
query_add( from, to, val, now << 1 | 1, mid + 1, rig );
pushup( now, left, rig );
calc( now, left, rig );
}3 例题
3.1 Luogu P1502 窗口的星星
因为坐标过大,需要离散化
这里的扫描线求的并不是矩形面积并
正常线段树即可
#include <cstdio>
#include <algorithm>
const int N = 11000;
int _case, Max_ans, xcnt;
int n, W, H;
int left[N], rig[N];
struct node{
int now, light, id;
bool fl;
}x[N << 1], y[N << 1];
bool cmp(node a, node b) {return a.now < b.now;}
bool cmp1(node a, node b) {return a.now == b.now ? a.light > b.light: a.now < b.now;}
inline int Max(int a, int b) {return a > b? a : b;}
inline void init(){ Max_ans = xcnt = 0; }
inline void readin(){
scanf("%d%d%d", &n, &W, &H);
for(int i = 1; i <= n; i++){
scanf("%d%d%d", &x[i].now, &y[i].now, &x[i].light);
y[i].id = x[i].id = i;
x[i].fl = y[i].fl = false;
y[i].light = x[i].light;
}
}
inline void get_pre(){
for(int i = 1; i <= n; i++){
x[i + n] = x[i];
x[i + n].now += W - 1;
x[i + n].fl = true;
y[i + n] = y[i];
y[i + n].now += H - 1;
y[i + n].light = -y[i].light;
}
std::sort(x + 1, x + (n << 1) + 1, cmp);
for(int i = 1; i <= (n << 1); i++){
if(i == 1 || x[i].now != x[i - 1].now) xcnt++;
if(!x[i].fl) left[ x[i].id ] = xcnt;
else rig[ x[i].id ] = xcnt;
}
std::sort(y + 1, y + (n << 1) + 1, cmp1);
}
// Segment Tree Start
int tree[N << 3], lazy[N << 3];
inline void pushup(int now){tree[now] = Max(tree[now << 1], tree[now << 1 | 1]);}
inline void pushdown(int now){
if(lazy[now]){
tree[now << 1] += lazy[now];
tree[now << 1 | 1] += lazy[now];
lazy[now << 1] += lazy[now];
lazy[now << 1 | 1] += lazy[now];
lazy[now] = 0 ;
}
}
void build_tree(int now, int left, int rig){
if(left == rig){
tree[now] = lazy[now] = 0;
return ;
}
int mid = (left + rig) >> 1;
build_tree(now << 1, left, mid);
build_tree(now << 1 | 1, mid + 1, rig);
tree[now] = lazy[now] = 0;
}
int query_Max(int now, int left, int rig, int from, int to){
if(from <= left && rig <= to){ return tree[now]; }
pushdown(now);
int mid = (left + rig) >> 1, res = 0;
if(from <= mid) res = Max(query_Max(now << 1, left, mid, from, to), res);
if(to > mid) res = Max(query_Max(now << 1 | 1, mid + 1, rig, from, to), res);
return res;
}
void query_add(int now, int left, int rig, int from, int to, int val){
if(from <= left && rig <= to){
tree[now] += val;
lazy[now] += val;
return ;
}
pushdown(now);
int mid = (left + rig) >> 1;
if(from <= mid) query_add(now << 1, left, mid, from, to, val);
if(to > mid) query_add(now << 1 | 1, mid + 1, rig, from, to, val);
pushup(now);
}
// Segment Tree End
void get_ans(){
build_tree(1, 1, xcnt);
for(int i = 1, tmp; i <= (n << 1); i++){
if(y[i].light > 0){
tmp = query_Max(1, 1, xcnt, left[ y[i].id ], rig[ y[i].id ]);
tmp += y[i].light;
Max_ans = Max(tmp, Max_ans);
}
query_add(1, 1, xcnt, left[ y[i].id ], rig[ y[i].id ], y[i].light);
}
printf("%d\n", Max_ans);
}
int main(){
#ifdef woshiluo
freopen("luogu.1502.in", "r", stdin);
freopen("luogu.1502.out", "w", stdout);
#endif
scanf("%d", &_case);
while(_case--){
init();
readin();
get_pre();
get_ans();
}
}3.2 树
这是一道校内模拟赛的训练题目,详见结题报告
#include <cstdio>
#include <algorithm>
inline int read() {
register char c = 0; register int now = 0;
while( c < '0' || c > '9' )
c = getchar();
while( c >= '0' && c <= '9' ) {
now = ( now << 3 ) + ( now << 1 ) + ( c - 48 );
c = getchar();
}
return now;
}
inline int Min( int a, int b ) { return a < b? a: b; }
inline int Max( int a, int b ) { return a > b? a: b; }
const int N = 1e5 + 10;
int n, m, scnt;
long long ans;
// Edge Start
struct edge {
int to, next;
} e[N << 2];
int ehead[N << 1], ecnt;
inline void add_edge( int now, int to ) {
ecnt ++;
e[ecnt].to = to;
e[ecnt].next = ehead[now];
ehead[now] = ecnt;
}
// Edge End
// Segment Tree Start
int tree[N << 2], tree_cnt[N << 2];
inline void push_up( int now, int left, int rig ) {
if( tree_cnt[now] )
tree[now] = ( rig - left + 1 );
else if( rig - left == 0 )
tree[now] = 0;
else
tree[now] = tree[ now << 1 ] + tree[ now << 1 | 1 ];
}
void query_add( int from, int to, int val, int now, int left, int rig ) {
if( from <= left && rig <= to ) {
tree_cnt[now] += val;
push_up( now, left, rig );
return ;
}
int mid = ( left + rig ) >> 1;
if( from <= mid )
query_add( from, to, val, now << 1, left, mid );
if( to > mid )
query_add( from, to, val, now << 1 | 1, mid + 1, rig );
push_up( now, left, rig );
}
// Segment Tree End
// Heavy-Light Decompostion Start
int fa[N], fir[N], last[N], son[N], mson[N], top[N], cnt;
void dfs1( int now ) {
fir[now] = ++ cnt; son[now] = 1;
for( int i = ehead[now]; i; i = e[i].next ) {
if( e[i].to == fa[now] )
continue;
fa[ e[i].to ] = now;
dfs1( e[i].to );
son[now] += son[ e[i].to ];
if( son[ mson[now] ] < son[ e[i].to ] )
mson[now] = e[i].to;
}
last[now] = cnt;
}
void dfs2( int now ) {
if( top[now] == 0 )
top[now] = now;
if( son[now] == 1 )
return ;
top[ mson[now] ] = top[now];
dfs2( mson[now] );
for( int i = ehead[now]; i; i = e[i].next ) {
if( e[i].to == fa[now] || e[i].to == mson[now] )
continue;
dfs2( e[i].to );
}
}
int get_son( int from, int to ) {
int tmp;
while( top[from] != top[to] ) {
tmp = top[from];
from = fa[ top[from] ];
}
if( from == to ) { return tmp; }
return mson[to];
}
// Heavy-Light Decompostion End
// Seq Start
struct seq {
int left, rig, y;
bool add;
} s[N * 16];
bool cmp( seq a, seq b ) { return a.y < b.y; }
inline void add_seq( int left, int rig, int low, int high ) {
if( left > rig || low > high ) {
return ;
}
int tmp = 0;
s[ ++ scnt ] = (seq) { left, rig, low, true };
s[ ++ scnt ] = (seq) { left, rig, high + 1, false };
s[ ++ scnt ] = (seq) { low, high, left, true };
s[ ++ scnt ] = (seq) { low, high, rig + 1, false };
tmp = Min( rig, high ) - Max( low, left ) + 1;
if( tmp > 0 )
ans -= 1LL * tmp;
}
// Seq End
int main() {
freopen( "tree.in", "r", stdin );
freopen( "tree.out", "w", stdout );
n = read(), m = read();
for( int i = 1, x, y; i < n; i++ ) {
x = read(), y = read();
add_edge( x, y );
add_edge( y, x );
}
dfs1( 3 );
dfs2( 3 );
for( int i = 1, x, y; i <= m; i++ ) {
x = read(), y = read();
if( fir[y] < fir[x] )
std::swap( x, y );
if( fir[x] <= fir[y] && fir[y] <= last[x] ) {
int tmp = get_son( y, x );
add_seq( fir[y], last[y], 1, fir[x]);
add_seq( fir[y], last[y], last[x] + 1, n );
add_seq( fir[y], last[y], fir[x] + 1, fir[tmp] - 1 );
add_seq( fir[y], last[y], last[tmp] + 1, last[x] );
}
else {
add_seq( fir[x], last[x], fir[y], last[y] );
}
}
std::sort( s + 1, s + scnt + 1, cmp );
int p = 1;
for( int i = 1; i <= n; i++ ) {
while( s[p].y <= i && p <= scnt ) {
if( s[p].left != 0 && s[p].rig != 0 )
query_add( s[p].left, s[p].rig, s[p].add? 1: -1, 1, 1, n );
p ++;
}
ans = ( ans + 1LL * tree[1] );
}
printf( "%lld\n", ( ( 1LL * n * ( n - 1 ) - ans ) >> 1LL ) );
}4 资料来源及致谢
笔者在学习和记录的时候,学习了以下博客及代码,在此处一并表示感谢