我怎么也沦落到发这种文章了。

整理都整理完了，不发白不发。

1 定义

给定两点 $F_1, F_2$，令 $|F_1F_2| = 2c$，存在动点 $P$ 满足 $|PF_1| + |PF_2| = 2a(2a>2c)$，则 P 的轨迹曲线为椭圆。

$2a = 2c$ 时 P 的轨迹为线段，也就是线段 $F_1F_2$；
$2a < 2c$ 时 P 不存在。

• $F_1, F_2$ 称为焦点。

---

第二定义：

准线：$x = \pm \frac{a^2}{c}$

令 $P$ 到左准线距离为 $d_1$，到右准线距离 $d_2$。

有

$$\frac{PF_1}{d_1} = \frac{PF_2}{d_2} = e ( e \in (0,1) )$$

2 几何性质

2.1 标准式

焦点在 $x$ 轴上：

$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 ( a > b > 0 )$$

焦点在 $y$ 轴上：

$$\frac{y^2}{a^2} + \frac{x^2}{b^2} = 1 ( a > b > 0 )$$

2.2 一般式

$$Ax^2 + By^2 = 1 (A>0,B>0,A \neq B)$$

• 注意 $A \neq B$ 不然就是圆了。

2.3 a, b, c 的关系

$$a^2 = b^2 + c^2$$

2.4 范围

$$x \in [-a,a], y \in [b,-b]$$

• $(a^2-e^2x_0^2)$
• 最大值：$x_0 = 0$ 时，取 $a^2$；
• 最小值：$x_0 = a$ 时，取 $a^2-c^2=b^2$。

2.5 对称性

关于坐标轴，$(0,0)$ 对称。

2.6 长短轴

• 长轴：$2a$
• 短轴：$2b$
• 焦距：$2c$
• 半焦距：$c$

2.7 离心率

表示椭圆的圆扁。

$$e=\frac{c}{a}$$

• 显然 $e \in (0,1)$ 因为 $a > c$

$e \to 1$，越扁。$e^2 = \frac{c^2}{a^2} = 1 – \frac{b^2}{a^2}$

2.7.1 求法

1. $e^2 = \frac{c^2}{a^2}$
2. 构建 $a,c$ 齐次式
3. 特殊位置特殊值
4. 焦点三角形底角 $\alpha, \beta$ 有 $e = \frac{\sin(\alpha + \beta)}{\sin \alpha + \sin \beta}$

注意范围

2.8 通径

过焦点，两端点位于椭圆上，垂直于 $x$ 轴的线段。

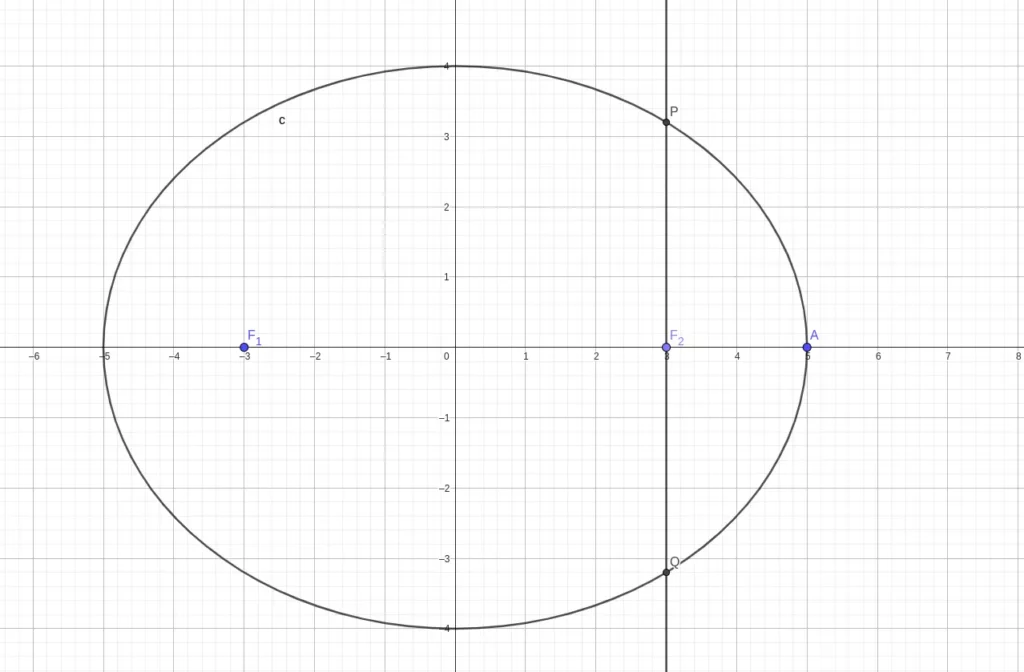
即图中 $PQ$。

有 $PQ = \frac{2b^2}{a}$

3 焦点

3.1 焦点三角形

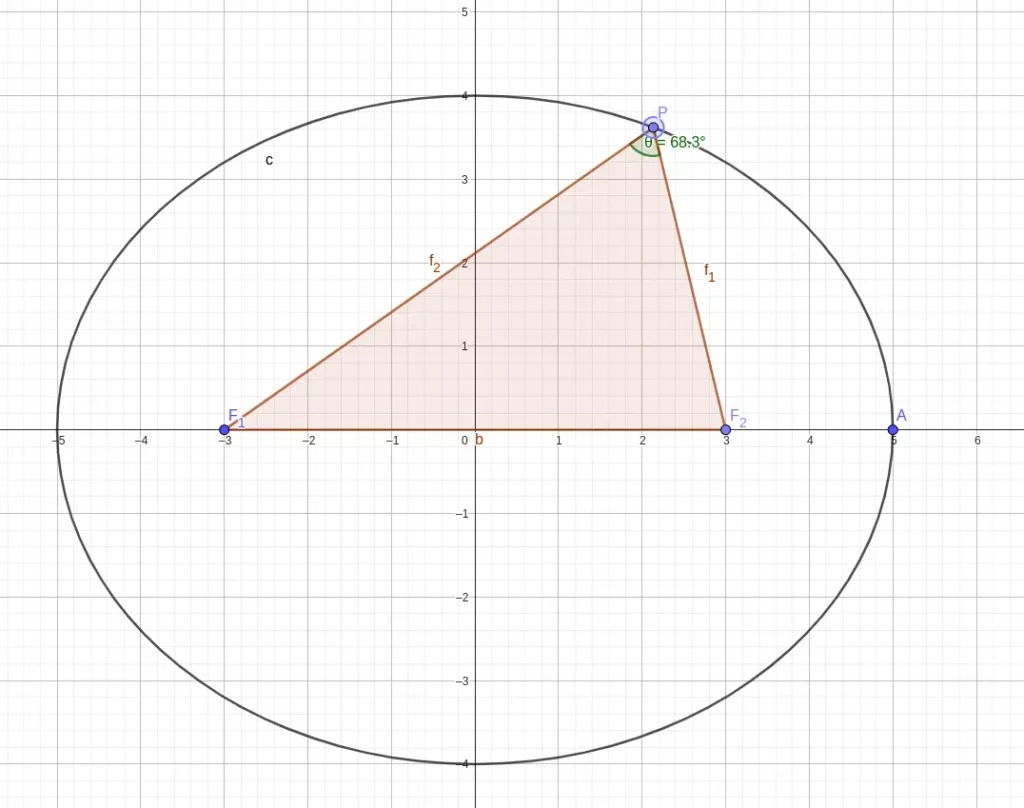
如图，以椭圆上一点 $P$ 和焦点 $F_1F_2$ 构成的三角形 $\triangle PF_1F_2$ 称为焦点三角形。

• $|PF_1|+|PF_2| = 2a$
• $|PF_1|^2 + |PF_2|^2 – 2|PF_1||PF_2| \cos \theta = |F_1F_2|^2 = 2c^2$
• $S \triangle = \frac{1}{2}|PF_1||PF_2| \sin \theta = b^2 \tan \theta$
• 周长： $2(c+a)$

3.1 延伸三角形

延伸焦点三角形中的非 $F_1F_2$ 一边交于椭圆，为延伸三角形。

• 周长：$4a$

3.2 焦半径

就是 $PF_1,PF_2$

有 $PF_1 = a + ex_0$ $PF_2 = a – ex_0$

代入第二定义证明。

有 $PF \in [ a – c, a + c ]$。

4 方程

4.1 共焦点

与

$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 ( a > b > 0 )$$

共焦点的椭圆可设

$$\frac{x^2}{a^2-k} + \frac{y^2}{b^2-k} = 1 ( a > b > 0, b^2 – k > 0 )$$

4.2 共离心率

与

$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 ( a > b > 0 )$$

共焦点的椭圆可设

$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = \lambda ( a > b > 0, \lambda > 0 )$$

5 公式

5.1 中点弦

若 $M(x,y)$ 为椭圆弦 $AB$ 的中点。

有 $k_{AB} \cdot k_{OM} = -\frac{b^2}{a^2}$

点差法：
有 $A(x_1,y_1), B(x_2, y_2)$ 在椭圆上，即
$$\begin{cases} \frac{x_1^2}{a^2} + \frac{y_1^2}{b^2} = 1 \\ \frac{x_2^2}{a^2} + \frac{y_2^2}{b^2} = 1 \end{cases}$$
两式做差有
$$\frac{x_1^2 – x_2^2}{a^2} + \frac{y_1^2 – y_2^2}{b^2} = 0$$
整理可得
$$\frac{y_1-y_2}{x_1-x_2} = -\frac{b^2(x_1+x_2)}{a^2(y_1+y_2)}$$

5.2 弦长公式

$y = kx + b$ 与椭圆交于 $A(x_1,y_1), B(x_2, y_2)$

有 $|AB| = \sqrt{1+k^2}|x_1 – x_2| = \sqrt{1+k^2}\sqrt{(x_1+x_2)^2-4x_1x_2} = \sqrt{1+\frac{1}{k^2}}\sqrt{(y_1+y_2)^2-4y_1y_2}$

5.3 切线方程

过椭圆上一点 $(x_0,y_0)$ 切线方程为 $\frac{x_0x}{a^2} + \frac{y_0y}{b^2} = 1$

过椭圆外一点 $P(x_0,y_0)$ 的两条，和椭圆的两个切点 $P_1,P_2$ 所在直线方程：

$$\frac{x_0x}{a^2} + \frac{y_0y}{b^2} = 1$$