我怎么也沦落到发这种文章了。
整理都整理完了,不发白不发。
1 定义
给定两点 $F_1, F_2$,令 $|F_1F_2| = 2c$,存在动点 $P$ 满足 $|PF_1| + |PF_2| = 2a(2a>2c)$,则 P 的轨迹曲线为椭圆。
$2a = 2c$ 时 P 的轨迹为线段,也就是线段 $F_1F_2$;
$2a < 2c$ 时 P 不存在。
- $F_1, F_2$ 称为焦点。
第二定义:
准线:$x = \pm \frac{a^2}{c}$
令 $P$ 到左准线距离为 $d_1$,到右准线距离 $d_2$。
有
$$ \frac{PF_1}{d_1} = \frac{PF_2}{d_2} = e ( e \in (0,1) )$$
2 几何性质
2.1 标准式
焦点在 $x$ 轴上:
$$
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 ( a > b > 0 )
$$
焦点在 $y$ 轴上:
$$
\frac{y^2}{a^2} + \frac{x^2}{b^2} = 1 ( a > b > 0 )
$$
2.2 一般式
$$ Ax^2 + By^2 = 1 (A>0,B>0,A \neq B)$$
- 注意 $A \neq B$ 不然就是圆了。
2.3 a, b, c 的关系
$$ a^2 = b^2 + c^2 $$
2.4 范围
$$
x \in [-a,a], y \in [b,-b]
$$
- $(a^2-e^2x_0^2)$
- 最大值:$x_0 = 0$ 时,取 $a^2$;
- 最小值:$x_0 = a$ 时,取 $a^2-c^2=b^2$。
2.5 对称性
关于坐标轴,$(0,0)$ 对称。
2.6 长短轴
- 长轴:$2a$
- 短轴:$2b$
- 焦距:$2c$
- 半焦距:$c$
2.7 离心率
表示椭圆的圆扁。
$$e=\frac{c}{a}$$
- 显然 $e \in (0,1)$ 因为 $a > c$
$e \to 1$,越扁。$e^2 = \frac{c^2}{a^2} = 1 – \frac{b^2}{a^2}$
2.7.1 求法
- $e^2 = \frac{c^2}{a^2}$
- 构建 $a,c$ 齐次式
- 特殊位置特殊值
- 焦点三角形底角 $\alpha, \beta$ 有 $e = \frac{\sin(\alpha + \beta)}{\sin \alpha + \sin \beta}$
注意范围
2.8 通径
过焦点,两端点位于椭圆上,垂直于 $x$ 轴的线段。
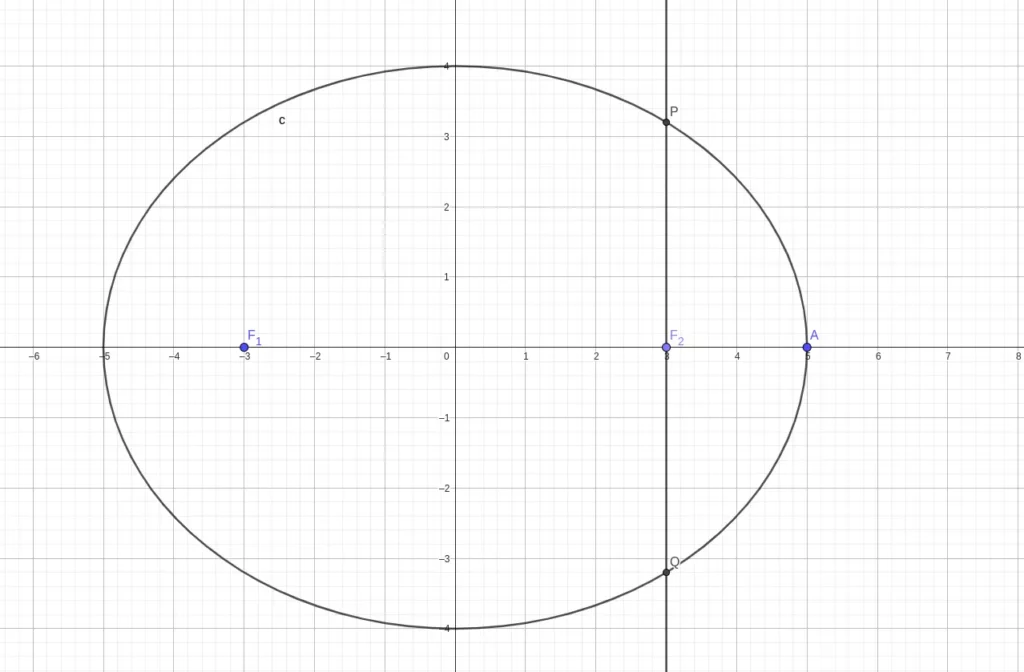
即图中 $PQ$。
有 $PQ = \frac{2b^2}{a}$
3 焦点
3.1 焦点三角形
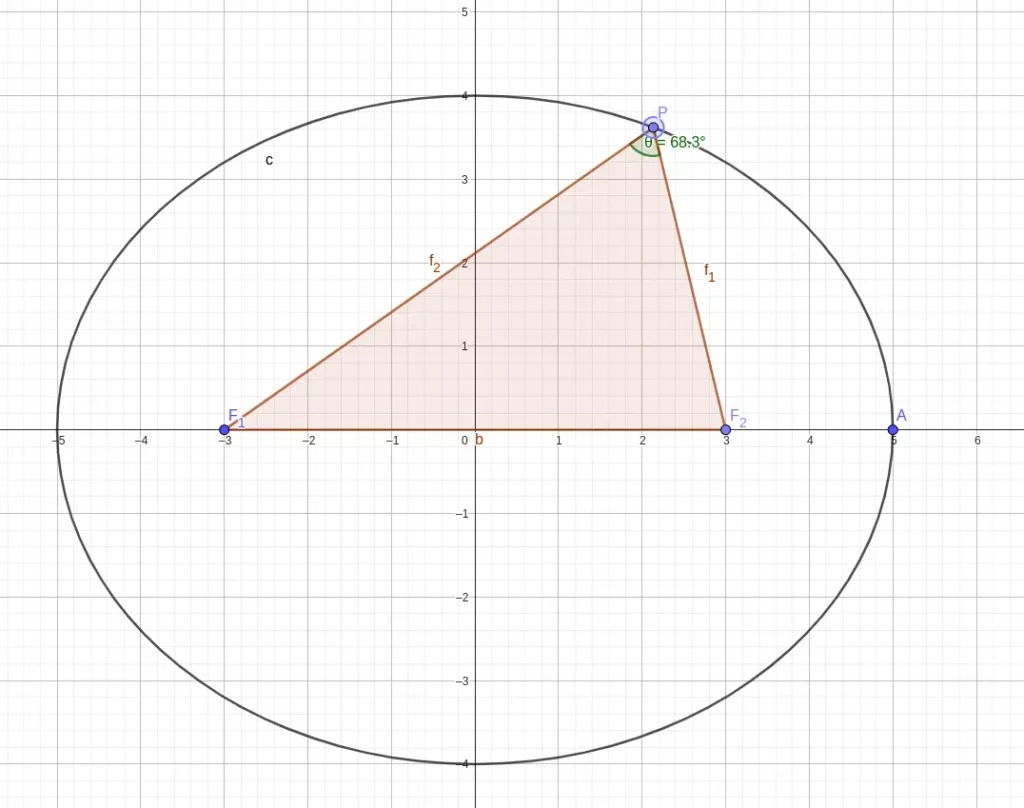
如图,以椭圆上一点 $P$ 和焦点 $F_1F_2$ 构成的三角形 $\triangle PF_1F_2$ 称为焦点三角形。
- $|PF_1|+|PF_2| = 2a$
- $|PF_1|^2 + |PF_2|^2 – 2|PF_1||PF_2| \cos \theta = |F_1F_2|^2 = 2c^2$
- $S \triangle = \frac{1}{2}|PF_1||PF_2| \sin \theta = b^2 \tan \theta$
- 周长: $2(c+a)$
3.1 延伸三角形
延伸焦点三角形中的非 $F_1F_2$ 一边交于椭圆,为延伸三角形。
- 周长:$4a$
3.2 焦半径
就是 $PF_1,PF_2$
有 $PF_1 = a + ex_0$ $PF_2 = a – ex_0$
代入第二定义证明。
有 $PF \in [ a – c, a + c ]$。
4 方程
4.1 共焦点
与
$$
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 ( a > b > 0 )
$$
共焦点的椭圆可设
$$
\frac{x^2}{a^2-k} + \frac{y^2}{b^2-k} = 1 ( a > b > 0, b^2 – k > 0 )
$$
4.2 共离心率
与
$$
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 ( a > b > 0 )
$$
共焦点的椭圆可设
$$
\frac{x^2}{a^2} + \frac{y^2}{b^2} = \lambda ( a > b > 0, \lambda > 0 )
$$
5 公式
5.1 中点弦
若 $M(x,y)$ 为椭圆弦 $AB$ 的中点。
有 $k_{AB} \cdot k_{OM} = -\frac{b^2}{a^2}$
点差法:
有 $A(x_1,y_1), B(x_2, y_2)$ 在椭圆上,即
$$\begin{cases} \frac{x_1^2}{a^2} + \frac{y_1^2}{b^2} = 1 \\ \frac{x_2^2}{a^2} + \frac{y_2^2}{b^2} = 1 \end{cases}$$
两式做差有
$$\frac{x_1^2 – x_2^2}{a^2} + \frac{y_1^2 – y_2^2}{b^2} = 0$$
整理可得
$$\frac{y_1-y_2}{x_1-x_2} = -\frac{b^2(x_1+x_2)}{a^2(y_1+y_2)}$$
5.2 弦长公式
$y = kx + b$ 与椭圆交于 $A(x_1,y_1), B(x_2, y_2)$
有 $|AB| = \sqrt{1+k^2}|x_1 – x_2| = \sqrt{1+k^2}\sqrt{(x_1+x_2)^2-4x_1x_2} = \sqrt{1+\frac{1}{k^2}}\sqrt{(y_1+y_2)^2-4y_1y_2}$
5.3 切线方程
过椭圆上一点 $(x_0,y_0)$ 切线方程为 $\frac{x_0x}{a^2} + \frac{y_0y}{b^2} = 1$
过椭圆外一点 $P(x_0,y_0)$ 的两条,和椭圆的两个切点 $P_1,P_2$ 所在直线方程:
$$\frac{x_0x}{a^2} + \frac{y_0y}{b^2} = 1$$
小猿的圆锥曲线书可以看一下
谢谢推荐
定义里 2a 和 2c 没有 latex!!
确实。改了。
通径错别字(另外通径应该是 2b^2 / a 吧。
fixed